탐색 : 문제의 해(solution)가 될 수 있는 것들의 집합을 공간(space)으로 간주하고, 문제에 대한 최적의 해를 찾기 위해 공간을 체계적으로 찾아 보는 것

상태 공간과 탐색
상태 공간(state space) : 문제 해결 과정에서 초기 상태로부터 도달할 수 있는 모든 상태들의 집합, 문제의 해가 될 가능성이 있는 모든 상태들의 집합
- 초기 상태 : 문제가 주어진 시점의 시작 상태
- 목표 상태 : 문제에서 원하는 최종 상태
상태 공간 그래프 : 상태(노드) 공간에서 각 행동(링크/간선)에 따른 상태의 변화를 나타낸 그래프
- 일반적인 문제에서는 상태 공간이 매우 큼
- 미리 상태 공간 그래프를 만들기 어려움
- 탐색과정에서 그래프 생성
맹목적 탐색
: 정해진 순서에 따라 상태 공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법
깊이 우선 탐색 (depth-first search, DFS) : 초기 노드에서 시작하여 깊이 방향으로 탐색
- 목표 노드에 도달하면 종료
- 더 이상 진행할 수 없으면, 백트랙킹
- 방문한 노드는 재방문 x
- 메모리에 대한 부담은 적지만 최단 경로를 찾는다는 보장이 없음

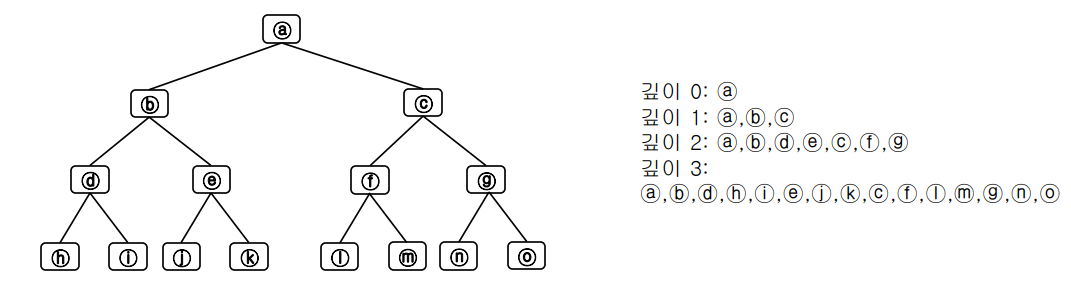
너비 우선 탐색 (breadth-first search, BFS) : 초기 노드에서 시작하여 모든 자식 노드를 확장하여 생성
- 목표 노드가 없으면 단말노드에서 다시 자식 노드 확장
- 메모리에 대한 부담은 크지만 최단 경로를 찾는다는 것을 보장함
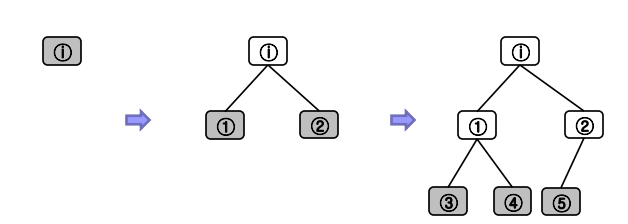
반복적 깊이심화 탐색 : 깊이 우선 탐색과 너비 우선 탐색의 장점 더함
- 깊이 한계가 있는 깊이 우선 탐색을 반복적으로 적용

양방향 탐색 : 초기 노드와 목적 노드에서 동시에 너비 우선 탐색을 진행
- 중간에 만나도록 하여 초기 노드에서 목표 노드로의 최단 경로를 찾는 방법

정보 이용 탐색
- 휴리스틱 : 시간이나 정보가 불충분하여 합리적인 판단을 할 수 없거나, 굳이 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 어림짐작하는 것
언덕 오르기 방법 : 현재 상태에서 주변(이웃) 중에서 가장 좋은 선택을 반복해서 목표를 찾는 방법
- 지역 탐색 : 현재 노드에서 확장 가능한 이웃 노드들 중에서 휴리 스틱에 의한 평가값이 가장 좋은 이웃 노드 하나를 확장해 가는 탐색 방법
- 그리디 알고리즘 : 현재 상황에서 가장 좋은 선택을 즉시 고르는 방식
- 국소 최적해 : 언덕 꼭대기인 줄 알았는데 사실 더 높은 언덕이 근처에 있는 상황

최상 우선 탐색 : 가장 가까워 보이는 길부터 탐색하는 방식

- 탐색 트리의 깊이가 깊어짐에 따라 확장될 수 있는 노드의 개수가 많아져 메모리 공간에 대한 부담 커짐
빔 탐색 : 휴리스틱에 의한 평가값이 우수한 일정 개수의 확장 가능한 노드만을 메모 리에 관리하면서 최상 우선 탐색을 적용

A* 알고리즘 : 추정한 전체 비용 𝑓 ̂(𝑛)을 최소로 하는 노드를 확장해 가는 방법
- 𝑓(𝑛) (전체비용 함수) : 노드 𝑛 을 경유하는 전체 비용
- 𝑓(𝑛) = 𝑔(𝑛)+ℎ(𝑛), 현재 노드 𝑛 까지 이미 투입된 비용 𝑔(𝑛) 과 목표 노드까지의 남은 비용 ℎ(𝑛) 의 합
- ℎ ̂(𝑛) (휴리스틱 함수) : 남은 비용 ℎ(𝑛) 은 정확히 알 수 없으므로 휴리스틱 값 ℎ ̂(𝑛) 로 대체
- 𝑓 ̂(𝑛): 추정 전체 비용 : 휴리스틱을 사용한 전체 경로의 추정치
- 𝑓 ̂(𝑛)=𝑔(𝑛)+ ℎ ̂(𝑛)


게임 트리 : 상대가 있는 게임에서 자신과 상대방의 가능한 게임 상태를 나타낸 트리
- 게임의 결과는 마지막에 결정
- 많은 수를 볼수록 유리
mini-max 알고리즘 : 단말 노드부터 위로 올라가면서 최소(minimum)-최대(maximum) 연산을 반 복하여 자신이 선택할 수 있는 방법 중 가장 좋은 것은 값을 결정, 휴리스틱 클수록 좋음
- MAX 노드 : 자신에 해당하는 노드로 자기에게 유리한 최대값 선택
- MIN 노드 : 상대방에 해당하는 노드로 최소값 선택

α-β 가지치기 (pruning) : 검토해 볼 필요가 없는 부분을 탐색하지 않도록 하는 기법
- 깊이 우선 탐색으로 제한 깊이까지 탐색을 하면서, MAX 노드와 MIN 노드 의 값 결정
- α-자르기(cut-off) : MIN 노드의 현재값이 부모노드의 현재 값보다 작거나 같으면, 나머지 자식 노드 탐색 중지
- β-자르기 : MAX 노드의 현재값이 부모노드의 현재 값보다 같거나 크면, 나머지 자식 노드 탐색 중지

제약조건 만족 문제
: 주어진 제약조건을 만족하는 조합 해(combinatorial solution)를 찾는 문제
백트랙킹 탐색 : 모든 가능한 값을 대입해서 만족하는 것이 없으면 이전 단계로 돌아가서 이전 단계의 변수에 다른 값을 대입
- 깊이 우선 탐색을 하는 것처럼 변수에 허용되는 값을 하나씩 대입

제약조건 전파 : 인접 변수 간의 제약 조건에 따라 각 변수에 허용될 수 없는 값들을 제거하 는 방식

최적화
: 여러 가지 허용되는 값들 중에서 주어진 기준을 가장 잘 만족하는 것을 선택 하는 것
- 목적함수 : 최적화 문제에서 우리가 최적화하려는 값
- 최적해(Optimal Solution): 주어진 제약조건을 만족하면서 목적함수의 값을 최대 또는 최 소로 하는 값
조합 최적화 : 순회 판매자 문제(TSP)와 같이 주어진 항목들의 조합으로 해가 표현되는 최 적화 문제

제약 조건 : 모든 도시 한번만 경유
순회 판매다 문제의 목적 함수 : 경로의 길이
문제의 해 : 도시 이름들의 순서
경사 하강법 : 함수의 최소값 위치를 찾는 문제에서 오차 함수의 그래디언트(gradient) 반대 방향으로 조금씩 움직여 가며 최적의 파라미터를 찾으려는 방법
- 데이터의 입력과 출력을 이용하여 각 파라미터에 대한 그래디언트를 계산 하여 파라미터를 반복적으로 조금씩 조정
- 국소해에 빠질 위험 있음
- 개선된 형태의 여러 방법 존재



'미쳤습니까 휴먼 (AI)' 카테고리의 다른 글
| [인공지능] 퍼셉트론 (0) | 2024.12.04 |
|---|---|
| [인공지능] 지식 표현과 추론 (1) | 2024.12.02 |
| [인공지능] 인공지능이란? (0) | 2024.09.21 |
| [AI 데이터 분석] Numpy와 Pandas와 Matplotlib 데이터 분석 (1) | 2022.08.24 |
| [AI 데이터 분석] 파이썬 모듈과 패키지 (0) | 2022.08.24 |



