Optimization (최적화): 손실함수의 값을 가능한 한 낮추는 매개변수의 최적값을 찾는 것
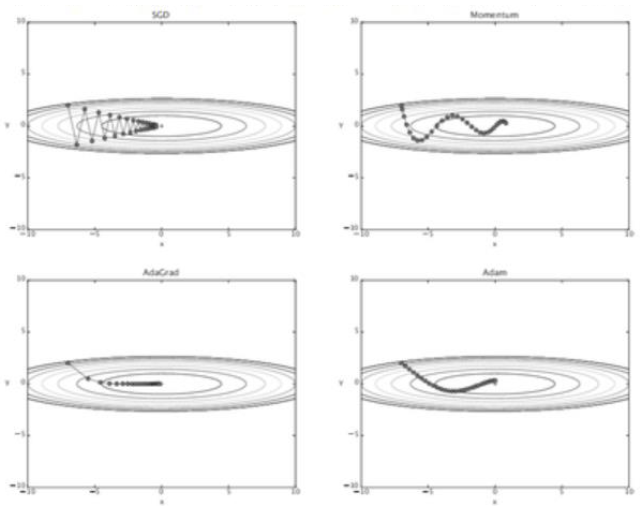
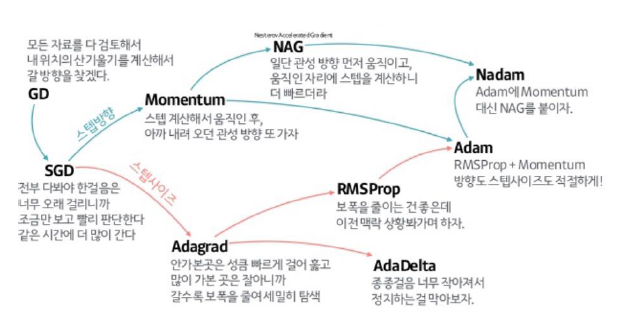
Stochastic Gradient Descent (확률적 경사 하강법): 매개변수의 기울기를 구해 기울어진 방향으로 매개변수 값을 갱신하는 일
- 기울어진 방향으로 일정 거리만 가는 방법
- W : 갱신할 가중치 매개변수
- n : 학습률
- L : W로 미분한 값, 손실함수의 기울기
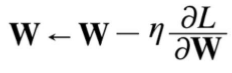
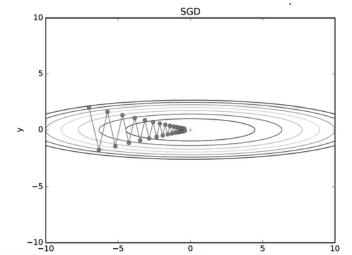
- 비등방성 함수에서는 탐색 경로가 비효율적
Momentum (모멘텀) : Gradient Descent를 통해 이동하는 과정에 일종의 ‘관성’을 주는 방법
- 현재 Gradient를 통해 이동하는 방향과는 별개로 과거에 이동했던 방식을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하는 방식
- 알파 : 얼마나 momentum을 줄 것인지에 대한 term
- 속도 : 과거에 얼마나 이동했는지에 대한 이동 항 v를 기억하고, 새로운 이동항을 구할 경우 과거에 이동했던 정도에 관성항 만큼 곱해준후 Gradient를 이용한 이동 step 합을 더해줌
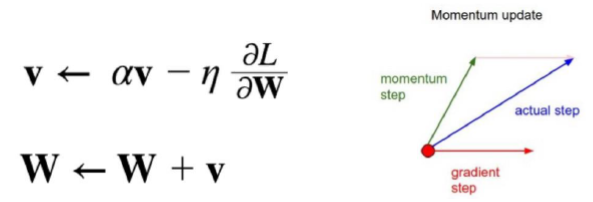
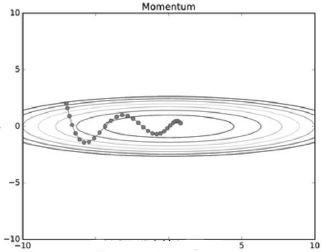
- 국소적 최적점을 빠져나오는 효과 기대
- 과거 이동했던 양을 변수별로 저장해야하므로 변수에 대한 메모리가 기존의 2배 필요
학습률(Learning Rate) : 학습 과정에서 모델이 가중치를 얼마나 빠르게 업데이트할지 결정하는 값
- 학습률이 너무 작으면 학습이 느려짐
- 학습률이 너무 크면 발산하여 학습이 제대로 이루어지지 않음
- 학습률 감소(Learning Rate Decay) : 학습을 진행하면서 학습률을 점차 줄여가는 방법
단순 방법(Simple Method): 모든 매개변수에 동일하게 전체 학습률을 낮춤
AdaGrad(= Adaptive Gradient) : 매개변수(변수)마다 학습률을 다르게 설정하여 더 효율적인 학습 진행
- 적게 변화한 변수: 큰 step size로 이동 (최적값에 도달하기 위해 빠르게 학습)
- 많이 변화한 변수: 작은 step size로 이동 (최적값 근처에서 세밀하게 조정)
- 자주 등장하거나 변화가 많은 변수들은 이미 최적값 근처일 확률이 높아, 작은 학습률로 정밀하게 이동
- 적게 변화한 변수들은 아직 최적값에서 멀리 있을 확률이 높아, 더 큰 학습률로 빠르게 이동
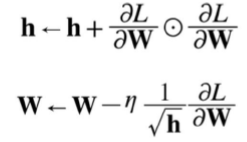
- 과거의 기울기를 제곱하여 계속 더해감으로써 학습을 진행할수록 갱신 강도가 약해짐
- 매개변수의 원소 중 크게 갱신된 원소는 학습률이 낮아짐 (= 학습률 감소가 매개변수의 원소마다 다르게 적용됨)
- 최소값에 도달하기 전에 학습률을 0에 수렴하게 만들 수 있음
RMSProp : AdaGrad의 단점을 해결하기 위한 방법
- AdaGrad식에서 gradient의 제곱값을 더해가면서 구한 h 부분을 합이 아니라 지수이동평균을 사용하여 최신 기울기들이 더 크게 반영되도록 함
- h가 무한정 커지지 않으면서 최근 변화량의 변수간 상대적 크기 차이는 유지할 수 있음
- Exponentially Weighted Moving Average (지수가중이동평균): 과거의 모든 기울기를 균일하게 더해가는 것이 아니라 먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영함
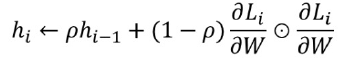
Adam (= Adaptive Moment Estimation) : Momentum + AdaGrad융합한 방법
가중치의 초깃값
가중치 감소 : 가중치 매개변수의 값이 작아지도록 학습하는 방법
- 가중치 값을 작게 하여 overfitting이 일어나지 않게 함
- Simple Method: 초기값을 최대한 작은 값으로 시작
- 초기값을 0으로 설정하면 (= 가중치를 균일한 값으로 설정하면), 오차역전파법의 모든 가중치 값이 똑같이 갱신되기 때문에 학습이 올바로 이뤄지지 않음 => 초기값을 무작위로 설정
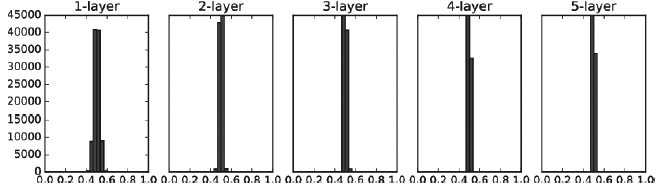
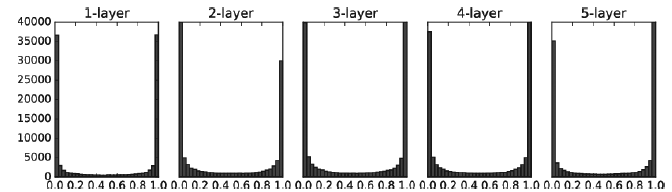
Gradient Vanishing (기울기 소실) : 데이터가 0과 1에 치우쳐 분포하면 역전파의 기울기 값이 점점 작아지다가 사라지게 됨
표현력 제한 : 다수의 뉴런이 거의 같은 값을 출력하는 상황은 뉴런을 여러 개 둔 의미가 없는 것과 동일한 의미
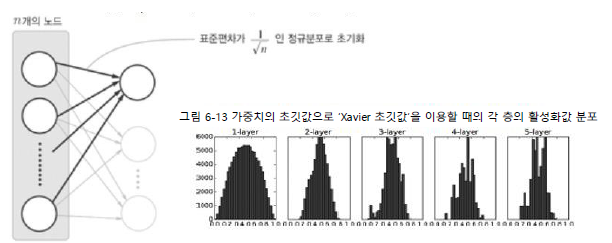
Xavier 초기값
- 전제조건: 활성화 함수가 대칭적 분포를 갖고 있음 (중앙 부분이 선형)
- 각 층의 활성화 값들을 광범위하게 분포시킬 목적으로 가중치의 적절한 분포를 찾음
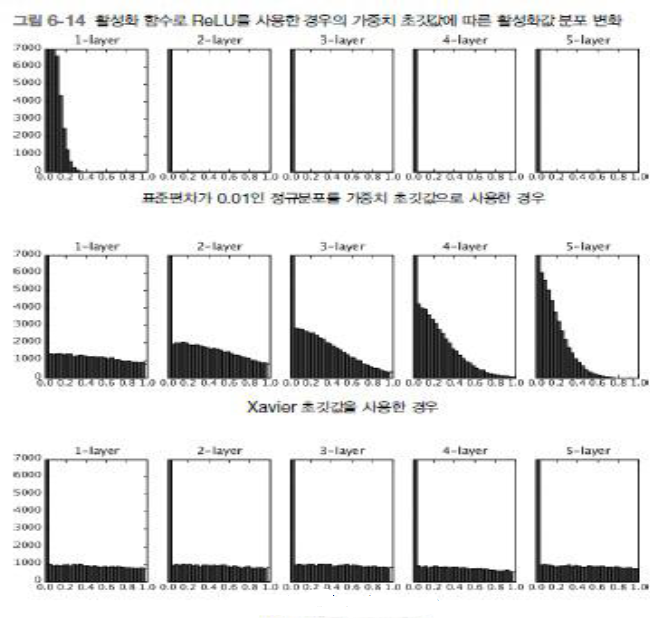
He 초기값 : ReLU함수를 사용할 때 사용하는 초기값: ReLU는 음의 영역이 0이라서 더 넓게 분포시키기 위해 2배의 계수가 필요함

MNIST 데이터셋으로 본 가중치 초깃값 비교
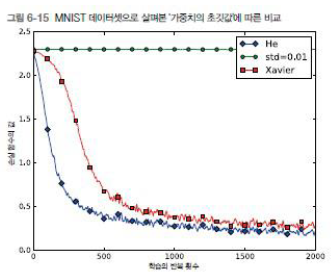
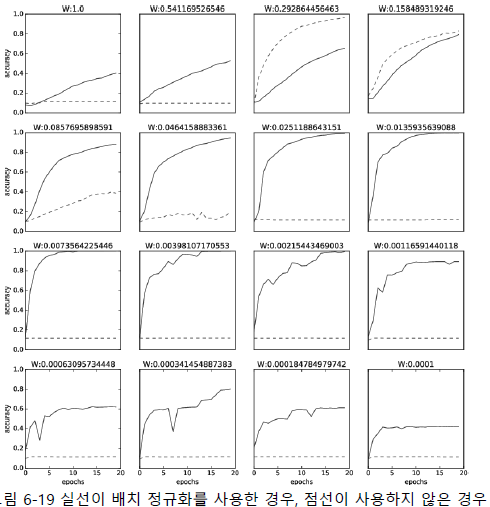
배치 정규화 (Batch Normalization) : 각 층에서의 활성화 값을 정규화하는 작업, 학습 시 미니배치를 단위로 정규화함 (데이터 분포가 평균 0, 분산 1이 되도록 정규화)
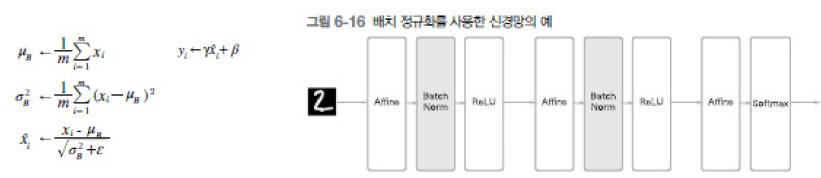
- 입력 분포의 균일화: 학습을 할 때 hidden layer의 중간에서 입력 분포가 학습할 때마다 변화하면서 가중치가 엉뚱한 방향으로 갱신될 문제가 발생할 수 있음
- 신경망의 층이 깊어질수록 학습 시에 가정했던 입력분포가 변화하여 엉뚱한 학습이 될 수 있음
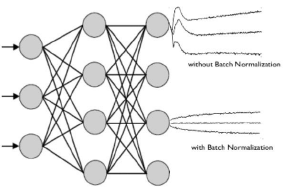
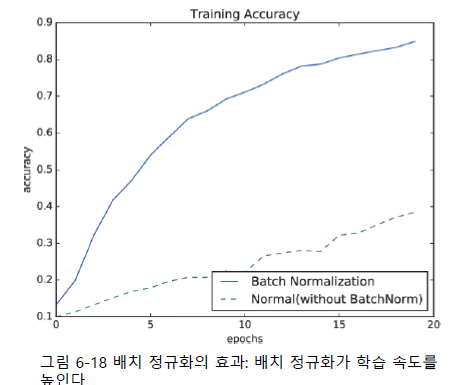
- 학습률을 높게 설정할 수 있으므로 학습 속도가 개선됨
- 학습할 때마다 출력값을 정규화하기 때문에 가중치 초깃값 선택에 의존성이 적어짐
- 드롭아웃 등의 필요성 감소: 오버피팅을 억제

학습할 때마다 출력값을 정규화하기 때문에 가중치 초깃값 선택에 의존성이 적어진다
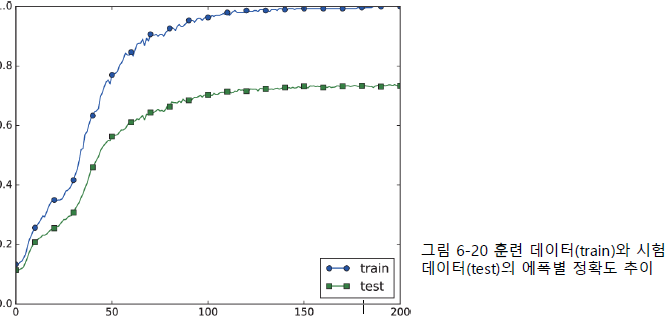
오버피팅 (Overfitting) : 신경망이 훈련 데이터에만 지나치게 적응되어 그 외의 데이터에는 제대로
대응하지 못하는 상태
- 매개 변수가 많고 표현력이 높은 모델
- 훈련 데이터가 적음
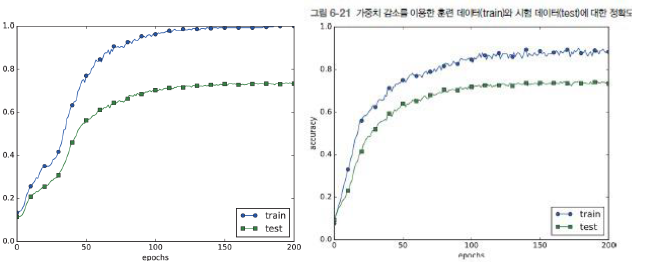
가중치 감소 (Weight Decay) : 학습 과정에서 큰 가중치에 대해서 그에 상응하는 큰 페널티를 부과하여 오
버피팅을 억제하는 방법
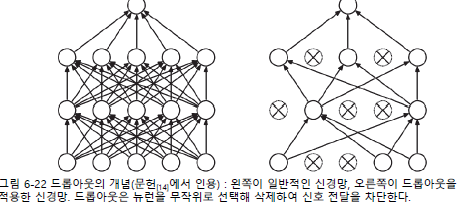
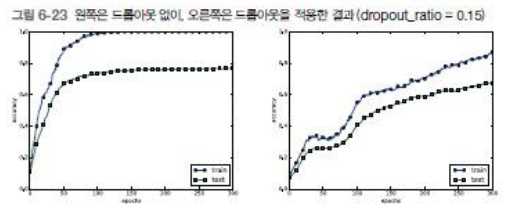
드롭아웃 : 뉴런을 임의로 삭제하면서 학습하는 방법
- 훈련 시, 은닉층의 뉴런을 무작위로 골라 삭제하고, 삭제된 뉴런은 신호를 전달하지 않게 됨
- 시험 시, 모든 뉴런에 신호를 전달함. 단, 시험 때는 각 뉴런의 출력에 훈련 때 삭제한 비율을 곱하여 출력함
- 드롭아웃 후 훈련 및 시험 데이터에 대한 정확도 차이가 줄었음
- 훈련데이터에 대한 정확도가 100%에 도달하지 않게 되었음
- 드롭아웃을 이용하면 표현력을 높이면서도 오버피팅을 억제할 수 있음
앙상블 학습(ensemble learning) : 개별적으로 학습시킨 여러 모델의 출력을 평균 내어 추론하는 방식
- 드롭아웃과 연관성: 드롭아웃이 학습 때 뉴런을 무작위로 삭제하는 행위를 매번 다른 모델을 학습시키는 것으로 해석 가능함
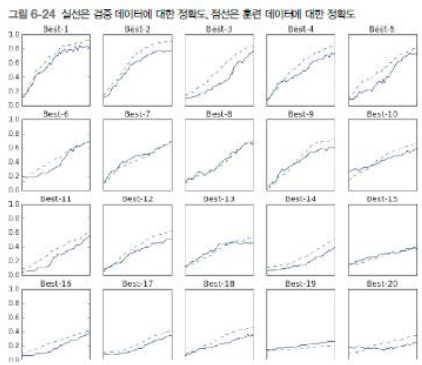
검증 데이터 (Validation Data) : 하이퍼파라미터 조정 시 모델의 성능을 평가하기 위해 사용
- 훈련 데이터 (Training Data): 모델의 매개변수(weights, biases 등) 학습에 사용.
- 검증 데이터 (Validation Data): 하이퍼파라미터 성능 평가에 사용
- 훈련 데이터의 약 20%를 검증 데이터로 분리
- 시험 데이터 (Test Data): 모델의 범용 성능을 최종 평가
- 시험 데이터를 사용해 하이퍼파라미터를 조정하면 시험 데이터에 과적합(overfitting) 될 위험이 있음.
- 따라서 훈련 데이터와 독립적인 검증 데이터를 활용해야 함.
하이퍼파라미터 최적화 (Hyperparameter Optimization)
0단계: 하이퍼파라미터 범위 설정
- 0.001 ~ 1,000의 Log Scale (10⁻³ ~ 10³) 활용.
1단계: 설정된 범위에서 하이퍼파라미터 값을 무작위로 추출
2단계: 1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고, 검증 데이터로 정확도를 평가
3단계: 1단계와 2단계를 특정 횟수 반복하며, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힘
'미쳤습니까 휴먼 (AI)' 카테고리의 다른 글
| [인공지능] 합성곱 신경망 (1) | 2024.12.05 |
|---|---|
| [인공지능] 오차역전파법 (0) | 2024.12.04 |
| [인공지능] 학습 알고리즘 (0) | 2024.12.04 |
| [인공지능] 신경망 (0) | 2024.12.04 |
| [인공지능] 퍼셉트론 (0) | 2024.12.04 |



