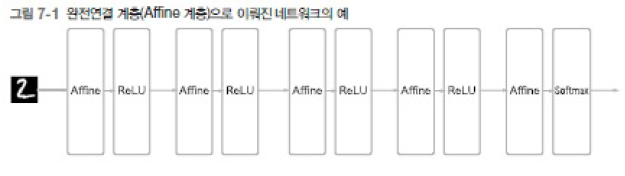
완전연결 (fully connected) : 신경망에 인접하는 계층의 모든 뉴련과 결합되어 있음
- Affine 계층 : 완전히 연결된 계층
- 단점 : 데이터의 형상이 무시됨 : 이미지는 가로 x 세로 x 채널 색상 로 구성된 3 차원 데이터인데 완전연결 계층에 입력할 때는 3 차원 데이터를 평평한 1 차원 데이터로 평탄화해줘야 함
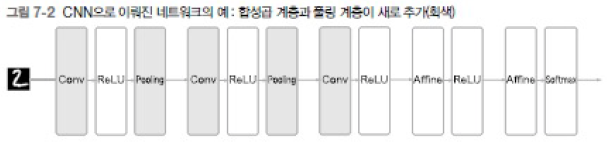
합성곱 신경망(CNN) : 합성곱 계층 (convolution layer)과 풀링 계층 (pooling layer)가 추가
- 합성곱 계층 : 형상을 유지함, 이미지도 3 차원 데이터로 입력받으며 , 다른 계층에도 3 차원 데이터를 전달함
- 입출력 데이터 : 특징맵 (feature map)
- 출력에 가까운 층에서는 Affine ReLU 구성을 사용할 수 있음
- 마지막 출력 계층에서는 Affine Softmax ’ 조합을 사용함
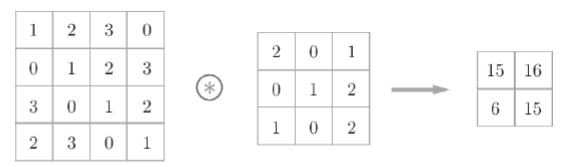
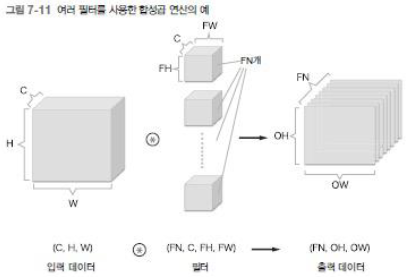
합성곱 연산 : 필터의 윈도우 ( 를 일정 간격으로 이동해가며 입력 데이터에 적용하고 , 입력과 필터에서 대응하는 원소끼리 곱한 후 그 총합을 구함, 영상처리의 필터 (filter, 커널 kernel) 연산과 동일함
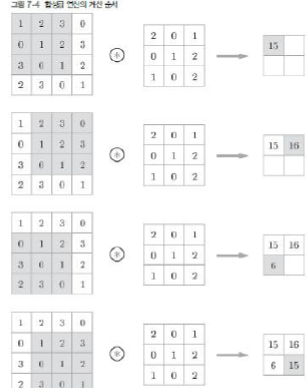
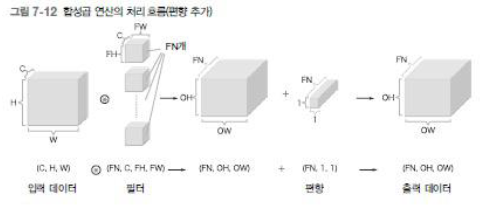
합성곱 연산의 편향 (bias)

패딩 (padding) : 합성곱 연산을 수행하기 전 입력 데이터 주변을 특정 값으로 채움으로써 출력 크기를 조정할 목적으로 사용함
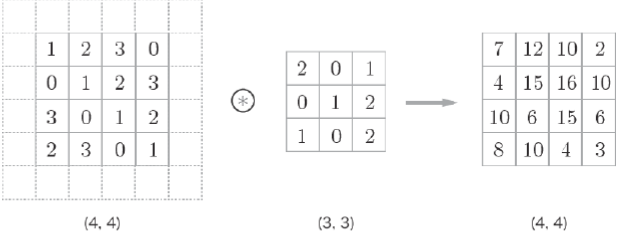
스트라이드 (stride) : 필터를 적용하는 위치의 간격으로 스트라이드를 키우면 출력크기는 작아짐, 패딩을 크게 하면 출력 크기가 커짐


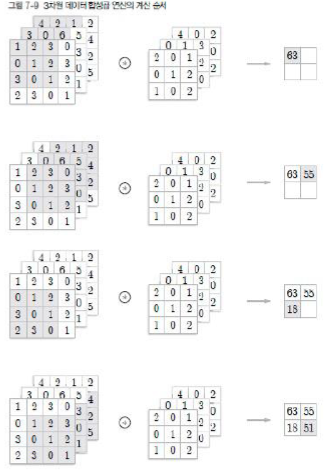
3 차원 데이터의 합성곱 연산
- 채널 쪽으로 특징맵이 여러 개 있다면 입력 데이터와 필터의 합성곱 연산을 채널마다 수행하고 , 그 결과를 더해서 하나의 출력을 얻음
- 입력 데이터의 채널 수와 필터의 채널 수가 같아야 함
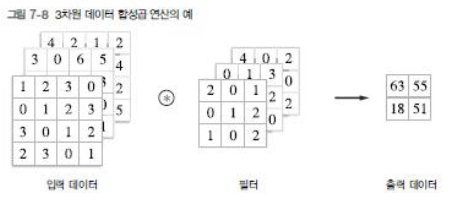
블록으로 생각하기
- 3 차원 데이터를 다차원 배열로 나타낼 때는 채널 channel , 높이 height 너비 width ) 순서로 사용하며 , 필터도 같은 순서를 사용함
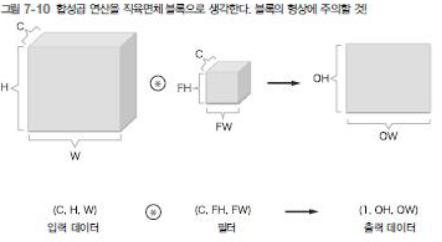
- 필터를 고려한 4 차원 데이터를 다차원 배열로 나타낼 때는 출력 채널 output channel , 입력채널 input channel , 높이 height , 너비 width ) 순서로 사용하며 , 필터도 같은 순서를 사용함
- 합성곱 연산에도 완전연결 계층과 마찬가지로 편향 (bias) 이 사용됨
- 각 계층을 흐르는 데이터의 차원을 하나 늘려 4 차원 데이터로 저장함 : 데이터 수 , 채널 수 , 높이 , 너비 ) 순으로 저장
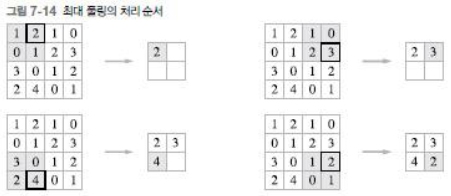
풀링 계층 (Pooling Layer) : 세로 , 가로 방향의 공간을 줄이는 연산
- 최대 풀링 (max pooling): 대상 영역에서 최대값 계산
- 평균 풀링 (average pooling): 대상 영역에서 평균 계산
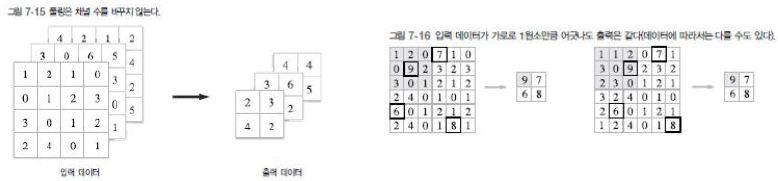
- 학습해야 할 매개변수가 없다
- 채널 수가 변하지 않는다
- 입력의 변화에 영향을 적게 받는다
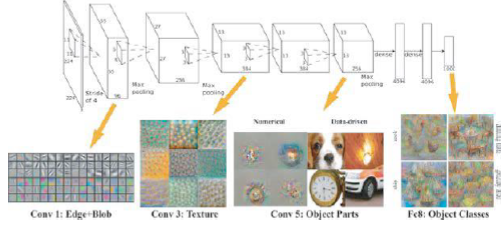
층 깊이에 따른 추출 정보 변화
1 번째 층의 합성곱 계층 : Edge 등의 저수준 정보 추출
3 번째 층의 합성곱 계층 : 텍스처 정보 추출
5 번째 층의 합성곱 계층 : 사물의 일부
대표적인 CNN
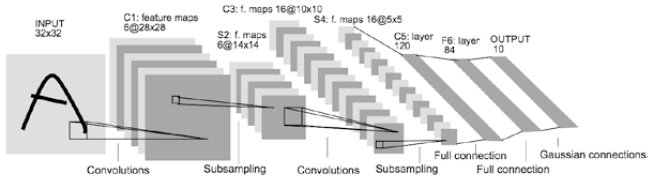
LeNet : 손글씨 숫자 인식하는 네트워크, 합성곱 계층과 풀링 계층을 반복하고 마지막으로 완전연결 계층을 거치면
서 결과를 출력함
- 활성화 함수 : Sigmoid 함수 , Subsampling 을 통한 feature map 줄이기
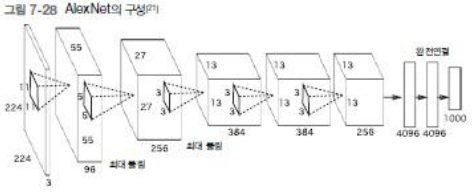
AlexNet : 2012 년 ILSVRC (ImageNet Large Scale Visual Recognition Challenge) 에서 Top5 test error 기준 15.4% 를 기록해 1 위를 차지
- 활성화 함수 : ReLU , 국소화 정규화 (LRN) 계층 및 드롭아웃 사용
'미쳤습니까 휴먼 (AI)' 카테고리의 다른 글
| [인공지능] 학습 관련 기술들 (1) | 2024.12.05 |
|---|---|
| [인공지능] 오차역전파법 (0) | 2024.12.04 |
| [인공지능] 학습 알고리즘 (0) | 2024.12.04 |
| [인공지능] 신경망 (0) | 2024.12.04 |
| [인공지능] 퍼셉트론 (0) | 2024.12.04 |
