블러링 : 마치 초점이 맞지 않은 사진처럼 영상을 부드럽게 만드는 필터링 기법이며 스무딩이라고도 불린다, 영상에서 인접한 픽셀 간의 픽셀 값 변화가 크지 않은 경우 부드러운 느낌을 받은 수 있다, 거친 느낌의 입력 영상을 부드럽게 만드는 용도를 사용되기도 하고, 입력 영상에 존재하는 잡음의 영샹을 제거하는 전처리 과정으로도 사용된다
블러링 필터 중 단순하고 구현하기 쉬운 필터는 평균값 필터이다. 평균값 필터는 입력 영상에서 특정 픽셀과 주변 픽셀들의 산술 평균을 결과 영상 픽셀 값으로 설정하는 필터이다. 평균 값 필터에 의해 생성되는 결과 영상은 픽셀 값의 급격한 변화가 줄어들어 날카로운 에지가 무너지고 잡음의 영샹이 크게 사라지는 효과가 있다

각각의 행렬은 모두 원소 값이 1로 설정되어 있고, 행렬의 전체 원소 개수로 각 행렬 원소 값을 나누는 형태로 표현되어 있다. 평균 값 필터는 마스크의 크기가 커지면 커질수록 더욱 부드러운 느낌의 결과 영상을 생성하며, 그 대신 연산량이 크게 증가할 수 있다
OpenCV에서는 blur() 함수를 사용해여 평균값 필터링을 수행할 수 있다.
void blurring_mean()
{
Mat src = imread("rose.bmp", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
imshow("src", src);
Mat dst;
//ksize 값이 3, 5, 7이 되도록 for 반복문 설정
for (int ksize = 3; ksize <= 7; ksize += 2) {
//ksize x ksize 크기의 평균 값 필터 마스크를 이용하여 블러링 수행
blur(src, dst, Size(ksize, ksize));
String desc = format("Mean: %dx%d", ksize, ksize);
putText(dst, desc, Point(10, 30), FONT_HERSHEY_SIMPLEX, 1.0,
Scalar(255), 1, LINE_AA);
imshow("dst", dst);
waitKey();
}
destroyAllWindows();
}



평균 값 필터의 크기가 커질수록 결과 영상이 더욱 부드럽게 변경되는 것을 확인할 수 있다
가우시안 필터 : 평균 값 필터보다 자연스러운 블러링 결과를 생성한다, 가우시안 분포 함수를 근사하여 생성한 필터마스크를 사용하는 필터링 기법이다
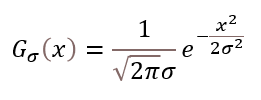
가우시안 분포는 평균을 중심으로 좌우 대칭의 종 모양을 갖는 확률 분포를 말하며 정규 분표라고도 한다.
OpenCV에서 가우시안 필터링을 수행하려면 GaussianBlur() 함수를 사용한다
void blurring_gaussian()
{
Mat src = imread("rose.bmp", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
imshow("src", src);
Mat dst;
//sigma 값을 5까지 증가시킨다
for (int sigma = 1; sigma <= 10; sigma++) {
//scr영상에 가우시안 표준 편차가 sigma인 가우시안 블러링을 수행
GaussianBlur(src, dst, Size(0, 0), (double)sigma);
String desc = format("Gaussian: sigma = %d", sigma);
putText(dst, desc, Point(10, 30), FONT_HERSHEY_SIMPLEX, 1.0,
Scalar(255), 1, LINE_AA);
imshow("dst", dst);
waitKey();
}
destroyAllWindows();
}




표준편차의 값이 커질수록 결과 영상이 더욱 부드럽게 변경되는 것을 확인할 수 있다
'런닝머신 (ML)' 카테고리의 다른 글
| [컴퓨터 비전 & 머신러닝] 잡음 제거 필터링 (0) | 2023.04.26 |
|---|---|
| [컴퓨터 비전 & 머신러닝] 샤프닝 : 영상 날카롭게 하기 (0) | 2023.04.24 |
| [컴퓨터 비전 & 머신러닝] 영상의 필터링 (0) | 2023.04.20 |
| [컴퓨터 비전 & 머신러닝] 영상의 논리 연산 (0) | 2023.04.18 |
| [컴퓨터 비전 & 머신러닝] 영상의 산술 연산 (0) | 2023.04.18 |



